Let's finally answer your question.
X elements arranged in Y groups with Z aspheric elements.
'X elements' is the number of individual lenses -- individual disks of glass.
'. . .arranged in y groups.' If you have two lenses placed together to effectively make a single lens, you would have x=2 lenses arranged in y=1 group. In other words, the difference between the x number and the y number is due to lenses held together to form doublets, triplets, etc. In earlier lens designs, individual lenses were often cemented together. Today they may be either cemented or air-spaced.
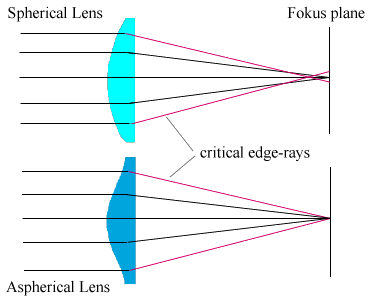
Aspheric has been discusses above. Lensmaking is easiest if the surface of the lens is a section of a sphere. The process of grinding and polishing a lens tends to produce a spherical surface almost automatically. When making a telescope mirror, as an example, the surface is first brought to a spherical surface and then slightly changed to a parabolic surface. A parabolic surface [actually a surface of revolution of a parabolic curve] is an aspheric surface -- a surface other than spherical. Another geometric surface other than a spherical surface would be a hyperbolic surface formed as the surface of revolution of an hyperbolic curve. It is more difficult to make a specific non-spherical surface and therefore it is avoided if possible. It is also more difficult to test an aspheric surface for accuracy than a comparable spherical surface.
In designing a lens, one problem is, of course, to focus the incoming wavelengths [colors] of light correctly. With a single lens, light of different wavelengths [red through violet] will come to a focus at different distances from the lens. For b&w film, the result is an unsharp image. For color film, the result is an unsharp image with a colored halo. This is known as chromatic aberration. There are different types of glass [crown and flint, eg] which have different effects on the focal distance of the various wavelengths of light. By choosing lenses of specific strengths [curvature] and types of glass, it is possible to bring all the wavelengths of visible light to a focus at almost the same distance from the lens. Such a lens is called an achromat -- a lens with little chromatic aberration as compared to a single lens.
This is a pretty problem with a lens with a single focal length, but it was solved rather neatly many years ago through such classic designs as the Zeiss Tessar, Schneider Xenon, etc. These lens designs are still excellent even by today's standards.
When you go to zoom lenses, however, you introduce an additional complication. The lens must still bring the various wavelengths to essentially the same focal point even when the lens focal length changes [achieved by changing the distance between some of the elements or groups.] This results in lens formulas with a much higher individual lens count [x]. Add in the requirement that the lens shall not require refocussing as the focal length changes [parfocal] and you have added yet another level of complexity. In some cases, the design problem is best solved through the use of one or more aspheric lens surfaces, even though the cost of production of that surface is higher than a spherical surface.
Finally, there is not only the problem of focussing the various wavelengths of light correctly, but you must also eliminate or reduce to an acceptable level five other types of lens aberrations!
Now, aren't you glad you asked? [heehee -- and also haha!!]
As an aside; when computing a lens formula for a single focal length lens, the fact that the lens can be stopped down eases the problem of equation solutions. Stopping down increases the depth of focus. You don't have to worry about the smaller lens stops quite so much. You can set up your design to maximize the correction at a large lens stop. Since you can assume that the lens will not be used wide open very often, it makes sense to maximize your solution for a stop 2 to 3 stops down from the maximum aperture. From thence comes the old rule of thumb on maximum sharpness.

 you are a good teacher.
you are a good teacher.





![[No title]](/data/xfmg/thumbnail/37/37603-739c5d9b541a083a12f2f30e45ca2b7b.jpg?1734170731)
![[No title]](/data/xfmg/thumbnail/37/37602-1ef8dbb1c2d0e4ff347ee65d328c3603.jpg?1734170730)



